Lasso Regression

회귀분석이란?

Lasso Regression 에서 뒤에 붙은 Regression 은 ‘회귀’를 뜻한다

회귀분석이란 무엇일까?

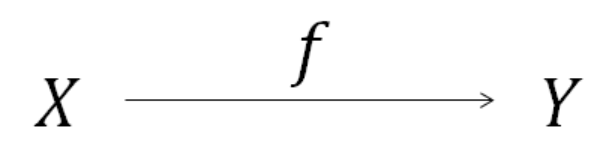
회귀분석이란 어떤 변수(Y)가 다른변수(X)에 의해 설명된다고 보고, 그 변수간의 관계(f)를 조사하는 해석방법이다.

만약 우리가 친구 상점의 판매량을 예측해야 한다고 가정하자.

판매량에 영향을 줄만한 변수는 무엇이 있을지 생각해보자. ‘매장의 크기’ 가 판매량에 강한 영향을 미칠 것이라고 생각할 수 있을 것이다.

그래서 매장들의 크기와 판매량을 기록해 보았더니 정말로 선형 관계가 있었다고 하자. 이를 이용해서 얻어낸 일차 함수식을 얻어낼 수 있을 것이고, 친구 상점의 매장 크기를 일차 함수식에 대입하여 판매량을 예측할 수 있을 것이다.

이것이 바로 선형회귀이다.

선형 회귀는 사용되는 특성의 갯수에 따라 단순 선형 회귀, 다중 선형 회귀로 분류할 수 있고, Lasso는 선형 회귀의 단점을 극복하기 위해 개발된 방법이다.

단순 선형 회귀

단순 선형 회귀란 단 하나의 특성을 가지고 타깃을 예측하는 것이다. 변수 하나를 가지고 하나의 변수를 예측한다.

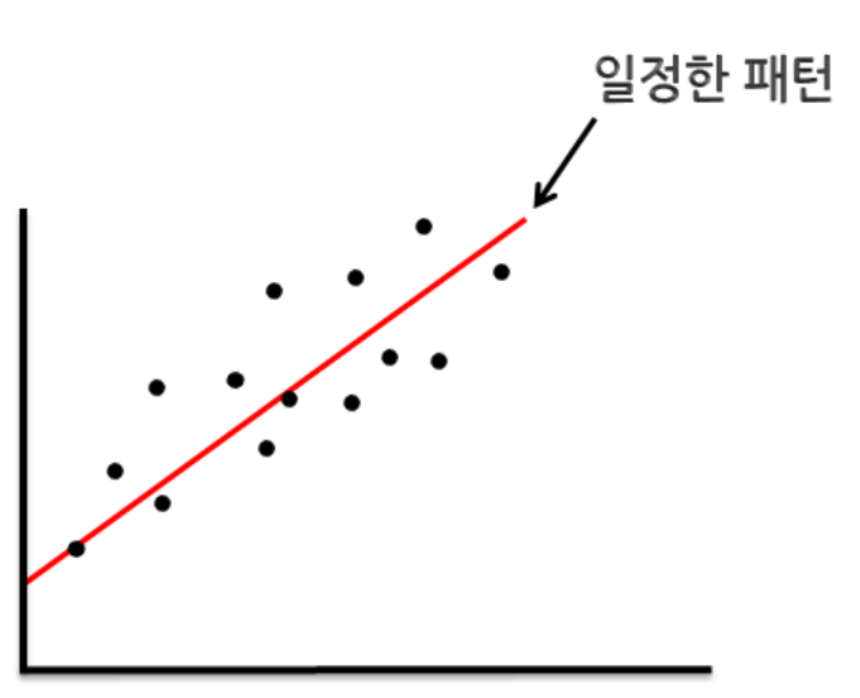
위의 그래프를 x축을 ‘매장 크기’, y축을 ‘판매량’으로 두고 친구 상점 주위 13개의 매장을 조사하여 찍은 데이터라고 하자. x값이 커지면 y값도 커지는 관계를 보이고 있다. 이러한 일정한 패턴을 가장 잘 설명해주는 선형 함수를 찾아낸 것이 빨간 선이다. 이렇게 선형 함수(빨간 선)을 찾아낸다면, 친구 매장의 크기를 가지고 판매량을 예측할 수 있을 것이다.

단순 선형 회귀를 위한 일반화된 함수는 다음과 같다

고등학교 수학에서 봤던 일차함수의 모양이지만, 여기서는 \(beta\)_\(1\)을 가중치(weight), $\beta_0$를 편향(offset) 이라고 부른다. 그리고 그냥 $y$ 가 아닌 $\hat{y}$인 이유는 $\hat{y}$가 실제 값이 아닌 추정값임을 나타내기 때문이다.

주어진 데이터에 완벽하게 딱 들어맞는 선형 함수를 찾아내는 것은 보통 불가능하다. 그리고 단 하나의 변수만 가지고 충분한 예측능력을 지닌 선형 함수를 만드는 것은 상당히 어렵다. 어떤 상점의 판매량에는 분명 ‘매장의 크기’뿐만이 아니라 ‘물건 보유량’ ,’세일하는 상품 수’ 등 수많은 변수들이 영향을 끼칠 것이기 때문이다.

다중 선형 회귀

그래서 하나의 변수가 아닌 여러개의 변수를 사용하여 회귀 모델을 만들고, 이것을 다중 선형 회귀라고 한다

다중 선형 회귀를 위한 일반화된 함수는 다음과 같다

위의 단순 선형 회귀와 비교했을때, 타깃 변수를 설명하는 변수가 두개 이상으로 증가한 것을 볼 수 있다. 타깃 변수를 설명하기 위한 변수는 $n+1$개이고 13개의 매장 데이터의 x값과 y값 사이의 관계를 잘 설명해낼 수 있는 $\beta$ 값들을 찾아야 할 것이다.

회귀식을 구하는 법

단순 선형 회귀와, 다중 선형 회귀에서 적절한 $\beta$ 값들, 즉 가중치와 편향을 찾는 방법은 다음과 같다. 어떤 한 x 값에 따른 실제 y 값과, x값을 회귀 함수에 넣었을때 나온 추정된 y 값의 차이가 최대한 작도록 회귀 함수를 구하는 것이다. 그래서 선형 회귀 함수는 실제 값($y$)과 추정값($\hat{y}$) 사이의 평균 제곱 오차(mean squared error, MSE)를 최소화하는 $\beta$ 값을 찾음으로서 구해진다.

MSE는 여러개의 x값에 따른 실제 값($y$)과 추정값($\hat{y}$) 사이의 차이를 제곱하고 그것들을 평균낸 값이다. 식으로 보는 편이 편할 것 같다

$MSE = {1 \over n} \sum _{i=1} ^n (y _{i} - {\hat{y}} _{i} ) ^{2}$ (여기서 $n$은 샘플 개수이다)

위 식에서 MSE 값이 최소가 되는 $\beta$값들을 찾으면 되는 것인데, MSE가 최소가 되었을때의 $\beta$는

$\underset{\beta}{\operatorname{arg min}} ({1 \over n} \sum _{i=1} ^n (y _{i} - {\hat{y}} _{i} ) ^{2})$ 요렇게도 표현 가능하다.

arg min을 설명하자면, $arg min(f(x))$는 $f(x)$를 최대로 만드는 $x$값이다. 예를 들어 $f(x) = cos(x)$일때 $arg min(f(x))$은 다음과 같다.

$\underset{0 \leq x \leq 2 \pi}{\operatorname{arg min}} (cos(x)) = {0, 2\pi}$

하지만 이렇게 구하면 과대적합(overfitting)이라는 문제가 생기게 되는데…!

overfitting

다중 선형 회귀에서 이용하는 변수가 2가지 일때와 6가지일때의 차이를 예시 그래프를 통해 보자.

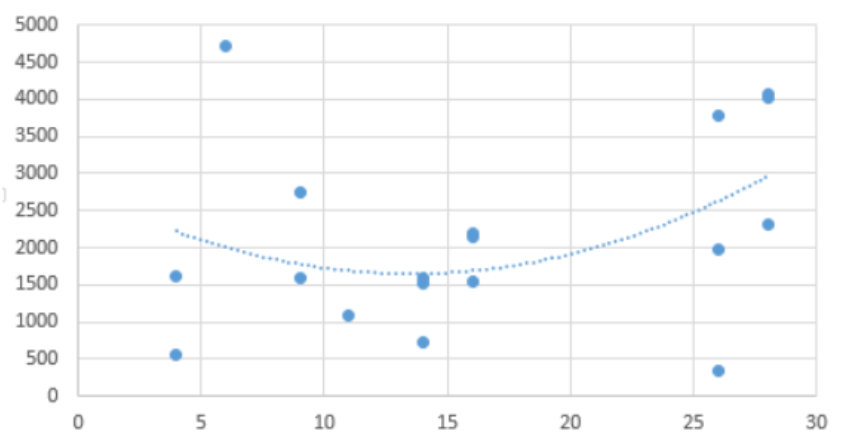
이 경우는 변수가 2가지일때이고,

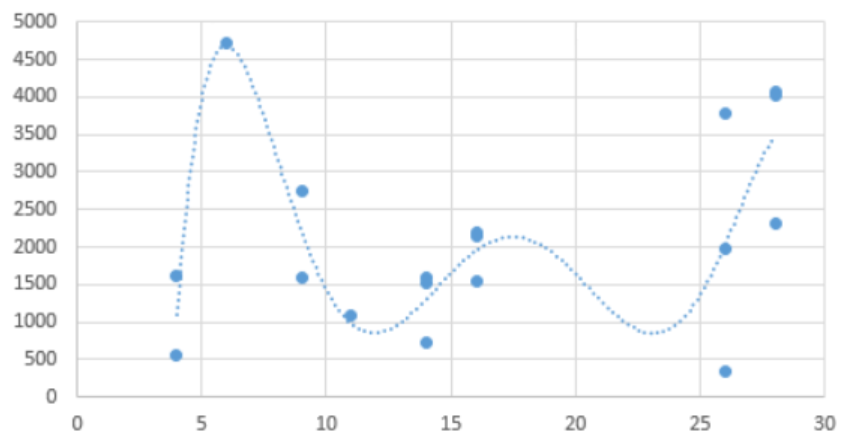
이 경우는 변수가 6가지일 때이다. 더 변수를 많이 쓸수록 더 데이터와 그럴듯하게 맞아 떨어지는 것을 볼 수 있다. 그렇지만 더 잘 맞아떨어진다고 해서 항상 변수 갯수를 많이! 회귀 함수를 고차원 방정식으로 사용해야 하는 것은 아니다. 위에서 그려진 6차 방정식은 train set(친구 동네의 다른 상점들)에 잘 맞는것일뿐, test set(친구 상점)에 에서는 잘 맞지 않을 수 있기 때문이다. 즉 일반화 능력이 떨어진다는 것인데 이러한 문제를 과적합(over-fitting)이라고 한다.

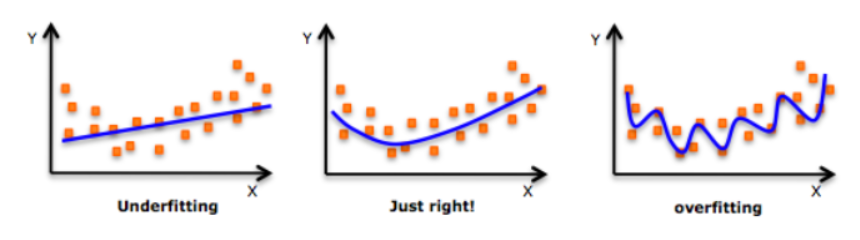
underfitting은 함수가 train set과 test set 모두에 맞지 않을 때이고, overfitting 은 다른 말로 함수가 “high variance”와 “low bias”를 가지고 있다고도 할 수 있다.

Variance? Bias?

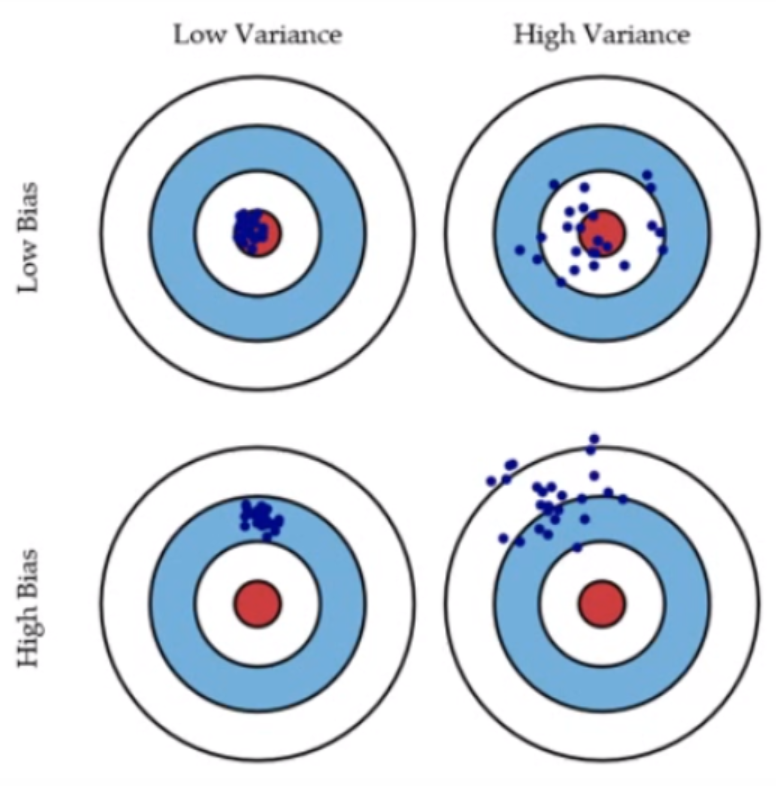
위의 양궁 과녁 예시 그림이 Variance와 Bias가 무엇인지 잘 설명해주고 있다. low bias, low variance를 가지고 있는 가장 좋은 경우가 왼쪽 위에 있는데, 여기서 variance가 증가하게되면 점들이 분산된 것을 볼 수 있다. 그리고 bias가 커지면 실제값(빨간색 원)과 추정값의 오차가 커지게 된다.

선형 회귀 모델에서는 실제값과 추정값의 오차를 줄이는 것에만 집중했기 때문에 bias는 작아졌지만, variance는 커질 수 있는 것이다.

아까 보았던 이 그림에서

Underfitting : low variance, high bias

Overfitting : high variance, low bias 인 것이다.

그렇다면 더 좋은 모델을 만들기 위해서는 bias와 variance가 어떻게 균형을 이루어야 할까?

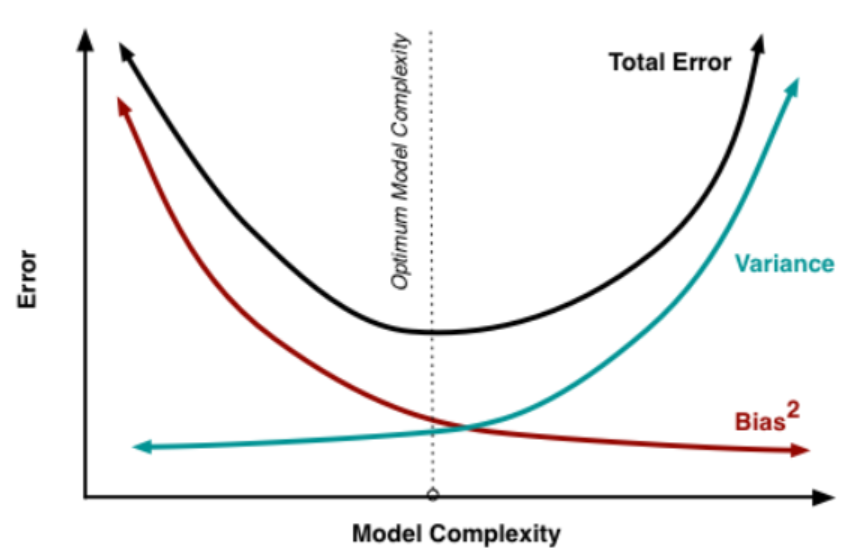
위의 그림을 보면, 우리가 모델을 만드는데 너무 적은 변수를 사용하게 되면 bias가 높게 된다 (underfitting). 그리고 너무 많은 변수를 사용하게 되면 모델의 복잡도는 올라가고 variance가 높아지게 된다 (overfitting). 따라서 우리는 저 점선이 표시하고 있는 최적 포인트에 가깝도록 모델을 만들어야 할 것이다.

underfitting을 해결하기 위해 변수를 추가할 수 있고, over fitting을 해결하기 위해서는 1. 모형의 복잡도를 줄이거나(변수 개수 줄이기) 2. 정규화(Regularization)을 할 수 있다. 그리고 정규화를 사용하는 회귀방법중 하나가 Lasso Regression이다.

정규화

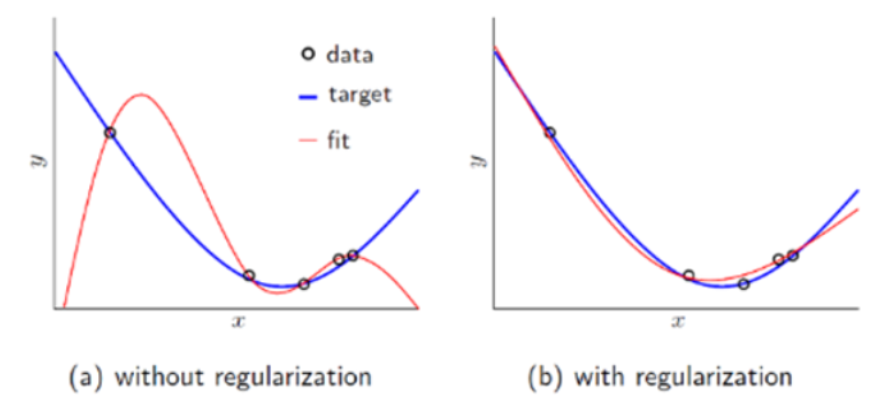
위의 그림은 정규화(Regularization)을 통해 더 좋은 결과를 가져오는 경우를 보여주는 그림이다.

Lasso regression은 정규화 중에서도 L1 Regularizaion 을 활용한다. L1 regularzation의 식은 다음과 같다

위 수식에서 $C_0$는 원래의 cost function, 즉 MSE이며, $n$은 데이터의 개수, $\lambda$는 regularization변수, $\beta$는 가중치를 나타낸다. 두번째 가중치 항은 ‘L1-penalty’라고도 한다. 위 식처럼 가중치 항이 추가되면 이 회귀 함수는 단순히 $C_0$을 최소화 하기위한 방향이 아니라 $\beta$ 값들 또한 최소가 되는 방향으로 만들어지게 된다.

이렇게 $\beta$ 값들이 작아지도록 회귀 함수를 만들면( = 정규화를 하고 나면), train-set의 “local noise”가 함수에 큰 영향을 끼치지 않으며, outlier(특이점)의 영향을 적게 받는다. 즉 함수를 일반화 시키고 overfitting 문제를 해결할 수 있게 된다!

Lasso regression 이란

그러니까 Lasso 모델은 L1 Regularization을 쓰는 선형 회귀 모형이다.

Lasso의 목적은 아래 수식과 같이 MSE와 L1-penalty 값의 합이 최소가 되게 하는 $\beta$ 값들을 찾는 것이다.

$\underset{\beta}{\operatorname{arg min}} (MSE + {L1 penalty})$

$= \underset{\beta}{\operatorname{arg min}} (MSE + {\alpha *L1 norm})$

$\alpha$는 패널티의 효과를 조절 해주는 파라미터인데, $\alpha$의 값이 커지면 패널티의 영향력이 커지고, $\alpha$의 값이 작아질수록 선형 회귀와 같아지는 것을 알 수 있다.

총 100개의 변수가 있는 데이터를 가지고 Lasso regression 모델을 만들었다고 하자.

$\alpha$를 1로 설정했을 때 : 100개의 $\beta$(가중치)중에서 96개가 0이 되면서 4개의 변수만 사용되었다. 이때의 결과는 underfitting이었다.

$\alpha$를 0.0001로 설정했을 때 : 94개의 변수가 사용되었고, 이때는 overfitting이 되었다.

$\alpha$를 0.1로 설정했을 때 : 33개의 변수가 사용되었고 가장 좋은 결과를 보였다

이런 식으로 $\alpha$값은 사용자가 cross-validation을 통해 적절한 값을 찾아서 설정해 주어야한다.

실습

실습에 사용할 데이터는 다양한 아울렛의 판매 정보를 담고 있는

The Big Mart Sales 데이터 셋이다.

실습을 위하여 기본 라이브러리들을 import 하고,

# import numpy as np
import pandas as pd
from pandas import Series, DataFrame
from sklearn.model_selection import train_test_split

파일을 불러와준 후 간단히 결측치 처리와 범주형 변수 더미화를 해주었다.

# import test and train file
train = pd.read_csv('Train.csv')
test = pd.read_csv('Test.csv')
# 결측치 처리
train['Item_Visibility'] = train['Item_Visibility'].replace(0, np.mean(train['Item_Visibility']))
train['Outlet_Establishment_Year'] = 2018-train['Outlet_Establishment_Year']
train['Outlet_Size'].fillna('Small', inplace = True)
train= train.dropna()
# 범주형 변수 더미화
dummy_list = list(train.select_dtypes(include =['object']).columns)
dummies = pd.get_dummies(train[dummy_list], prefix = dummy_list)
train.drop(dummy_list, axis = 1, inplace = True)
X = pd.concat([train, dummies], axis = 1)

Cross validation을 위해 train set을 나눠주었다

# 타깃 변수 지우기
X = X.drop('Item_Outlet_Sales',axis =1)
# splitting into training and cv for cross validation
x_train, x_cv, y_train, y_cv = train_test_split(X, train.Item_Outlet_Sales, test_size = 0.3)

$\alpha$에 따른 함수의 변화 보기

위에서 처리한 데이터에서 20개의 변수를 사용하여 Lasso regression 모델을 만들었다. 그리고 다음 코드를 통해서 각 변수별 가중치를 그래프에 나타내 보았다.

import matplotlib 
# 20개의 변수만 사용하기위해 처리해주었다
X = pd.concat([train, dummies], axis = 1).drop('Item_Outlet_Sales', axis =1 )
X_columns = X.columns
X = X[X_columns[:20]]
# splitting into training and cv for cross validation
x_train, x_cv, y_train, y_cv = train_test_split(X, train.Item_Outlet_Sales, test_size = 0.3)
predictors = x_train.columns

$\alpha$값을 0.05로 설정했을때 :

lassoReg = Lasso(alpha=0.005, normalize = True)
lassoReg.fit(x_train, y_train)
coef = Series(lassoReg.coef_, predictors).sort_values()
coef.plot(kind = 'bar');

그래프를 보면 3개의 변수가 사용되지 않았고 17개의 변수가 사용된 것을 알 수 있다.

$\alpha$ 값을 0.7로 설정했을때 :

lassoReg = Lasso(alpha=0.7, normalize = True)
lassoReg.fit(x_train, y_train)
coef = Series(lassoReg.coef_, predictors).sort_values()
coef.plot(kind = 'bar');

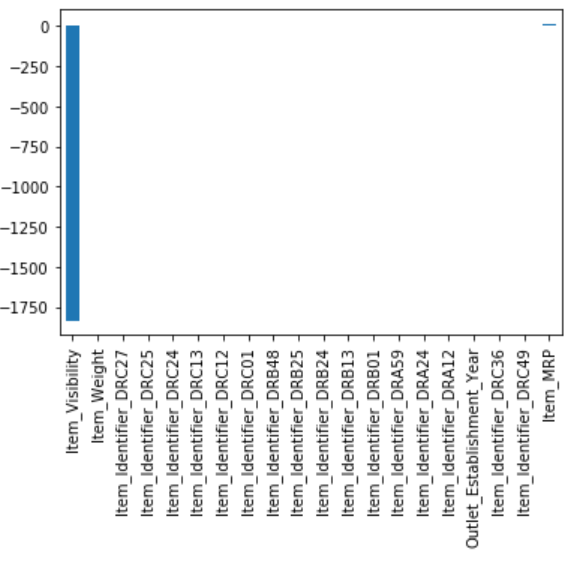
$\alpha$값을 높이니 패널티의 영향력이 커져서 가중치를 최소화 하다보니 변수가 2개(거의 1개인듯)밖에 남지 않게된 것을 볼 수 있다.

Linear Regression

선형 회귀분석 부터 먼저 해보자면..

# importing linear regression from sklearn
from sklearn.linear_model import LinearRegression
lreg = LinearRegression()
# training the model
lreg.fit(x_train, y_train)
# evaluation using r-square
lreg.score(x_cv, y_cv)

r-square를 통해 이 모델이 타깃 변수를 얼마나 설명할 수 있는지 확인할 수 있고, 이 값은 .score 함수를 통해 볼 수 있다. 이 값이 1일수록 잘 설명한다는 뜻이다. 그리고 Linear Regression을 사용했을때 나온 R-square의 값은..

-1666867036038316.5

음? r-square 값은 0에서 1사이의 값을 나타낸다고 했는데, 왜 이런일이.. 검색해보니 모델이 horizontal line보다도 잘 예측하지 못할때 마이너스 값이 나올 수 있다고 한다..

Lasso Regression

Lasso Regression을 import한후 train 해주었다.

이때, $\alpha$ 값은 0.005로 해보았다

# importing Lasso Regression from sklearn
from sklearn.linear_model import Lasso
lassoReg = Lasso(alpha=0.005, normalize = True)
# training the model
lassoReg.fit(x_train, y_train)
# evaluation using r-square
lassoReg.score(x_cv, y_cv)

아까와 마찬가지로 r-square 값을 구해보자

0.26097022661576019

오오..! $\alpha$값을 바꿔본다면..?

# importing Lasso Regression from sklearn
from sklearn.linear_model import Lasso
lassoReg = Lasso(alpha=0.5, normalize = True)
# training the model
lassoReg.fit(x_train, y_train)
# evaluation using r-square
lassoReg.score(x_cv, y_cv)

$\alpha$ 값이 대략 0.5일때 가장 스코어가 높았고.. 그 스코어는..!

0.48922716872909811

오오 올랐다!

Lasso의 장단점

• 장점

  • Lasso와 매우 유사하지만 $\beta$값이 절대 0이 될 수는 없는 Ridge regression과 비교했을 때, 변수의 개수를 줄일 수 없는 Ridge 와 달리 Lasso는 변수의 개수를 줄이고, 모델의 복잡성을 줄여서 모델 성능을 개선시킬 수 있다.
  • 변수가 많은데 그중 일부분만 중요할때 용이함

• 단점

  • 변수들끼리 correlate 한 경우에, Lasso는 단 한개의 변수만 채택하고 다른 변수들의 계수는 0으로 바꿀 것이다. 이렇게 정보가 손실됨에 따라 정확성이 떨어질 수 있다.
  • 변수들의 중요도가 전반적으로 비슷한 경우에 효과적이지 못함

• 그렇다면..?

  • Elastic Net Regression : 또 다른 유형의 regression이 존재한다. Ridge와 Lasso의 하이브리드 형태.

참고자료